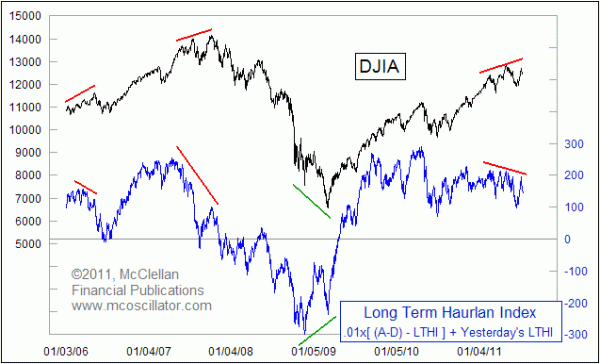
The Long Term Haurlan Index is showing a big divergence now, similar to ones that we have seen at past instances of impending stock market turmoil. That is the important part of the story in this week's chart.
But the history of this indicator and its creator is also a really interesting story. The Haurlan Index is now a little known indicator used by a handful of technicians, but when it was introduced in the 1960s it got a lot of attention. It arguably still deserves that same amount of attention, even though we now have many more tools we can choose among.
P.N. (Pete) Haurlan was an actual rocket scientist who worked for the Jet Propulsion Laboratory in Pasadena, CA in the early 1960s. Haurlan served as manager of the Advanced Technical Studies section under Fred Felberg, and helped envision several future missions including Venus/Mercury, Jupiter Gravity-Assist, and near-asteroid visits.
He also loved the stock market, and so during the late night hours when JPL's computer was not busy, he used it to do analysis on stock prices. Try to imagine punching in price data onto a stock of IBM cards (remember hanging chads?), and then loading those into the hopper to have the computer read them and do calculations. This was the state of the art for computerized technical analysis in the 1960s.
Haurlan's work led him to start the Trade Levels newsletter in the mid-1960s. It differed from the other newsletters of the day in that it had computer generated charts and statistics. Trade Levels was the sponsor of Gene Morgan's end of day TV program called "Charting The Market" on KWHY-TV in Los Angeles, a show which introduced thousands of people to the idea that a person could look at a chart of price movements, and derive useful information from it. That idea ran contrary to the conventional wisdom at that time.
Haurlan was also the first person (to our knowledge) to introduce the use of exponential moving averages for tracking stock prices. It was a piece of mathematics which he borrowed from his work in rocketry. EMAs were employed in the design of analog tracking circuitry because they made for easier designs. To calculate a 50-day simple moving average, for example, one must keep track of the last 50 data points, which was a lot of work for the early computers. For an exponential moving average calculation, the computer just needs to know the current data value, the prior EMA value, and the smoothing constant to apply to the new data.
For more background, see:
Who First Came Up With Moving Averages?
Exponential Moving Average Calculation
Who First Came Up With Moving Averages?
Exponential Moving Average Calculation
In his Trade Levels Report, Haurlan included an indicator he called the Haurlan Index. There were actually 3 versions of this indicator, for short, intermediate, and long term timing purposes. Each one looked at the daily Advance-Decline (A-D) difference, and used different smoothing factors to incorporate that data into an indicator.
From a 1972 issue of the Trade Levels report, Pete Haurlan defined the Haurlan Index as follows:
HI = K x (P - I)
Where I = previous day's Haurlan Index
P = NYSE Advances minus Declines
K = 50% for Short Term
10% for Intermediate Term
1% for Long Term
HI = K x (P - I)
Where I = previous day's Haurlan Index
P = NYSE Advances minus Declines
K = 50% for Short Term
10% for Intermediate Term
1% for Long Term
So each day's value for the Haurlan Index changes by a fraction of the difference between the A-D number and yesterday's Haurlan Index value.
The chart at the top of this article shows the Long Term Haurlan Index, which uses the 1% smoothing factor. It should be understood that the math involved is similar to the calculation of an exponential moving average, but it is not quite the same.
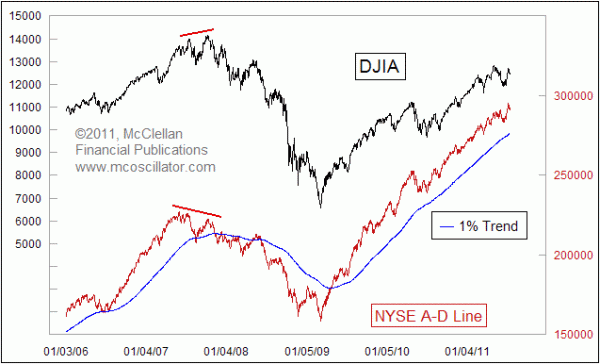
The 1% Trend is a nice long term moving average for the A-D Line, and for price indices as well. One additional tool that we like to look at is the distance between the A-D Line and the 1% Trend, or indeed any other moving average. We call this distance the "1% Trend Deviation", meaning how far prices have deviated away from that moving average.
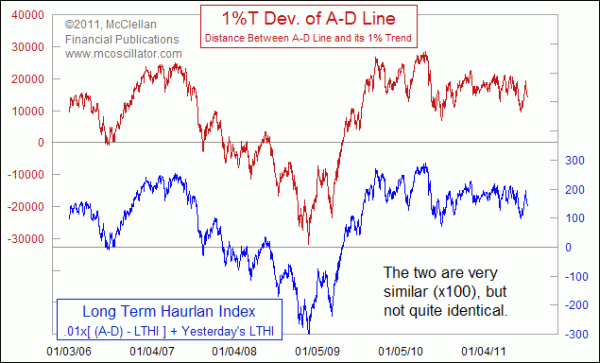
This is the interesting discovery: It turns out that the two indicators are nearly identical. On a chart, they are indistinguishable, and in the calculations the two are very close together, if we apply a multiplication factor of 100. This is part of the magic of the math involved with calculations involving exponential moving averages.
The Key Takeaway
While the NYSE's A-D Line is still making higher highs right now, the Long Term Haurlan Index is showing a significant divergence relative to prices. This is similar to divergences we are seeing elsewhere, such as in the McClellan A-D Summation Index that is featured in our twice monthly newsletter. These divergences are saying that even though the A-D Line may be making higher highs, it is not doing so with the same degree of vigor, which can be a setup for a meaningful intermediate to long-term correction.
Epilogue
Pete Haurlan passed away in the late 1970s, and for several years the Trade Levels Report was continued by the late David Holt, who later went on to be research chief at Wedbush Morgan. It says something interesting about the era that in a February 1980 issue, the authors still included this caveat:
"Data has been prepared largely by computer. Because of schedule requirements and the magnitude of the task, it is not possible to check thoroughly. Therefore, there may be errors and omissions."
These days, we do not think much about the idea that a few decades ago, there was far less trust of data that came out of a computer, without any human eyes making sure it was all okay. Times surely have changed.
The computer data may or may not be any more accurate now than it was in 1980, but we are all more accustomed to the idea of consuming such data.
Paul Carroll wrote about the 3 versions of the Haurlan Index in an article which appeared in the January 1994 issue of Technical Analysis of Stocks and Commodities.
No comments:
Post a Comment